페이딩 채널에서 확률 질량 함수를 이용한 인터리빙 파라미터 블라인드 추정

Ⅰ. 서 론

무선 채널에서는 송신된 신호가 건물이나 지형 지물의 영향으로 인하여 반사, 회절, 산란되어 시간차를 두고 수신되며 이로 인해 수신 전력의 크기가 커지거나 작아지는 다중 경로페이딩이 발생하게 된다. 통신 채널에서 발생하는 페이딩은 시스템의 수신 성능을 저하시키며 이를 보완하기 위한 여러 가지 기법들이 사용된다. 오류 정정 부호(Error Correction Code)는 이러한 기법중의 하나로서 채널에서 발생하는 랜덤 오류(Random Error)의 정정이 가능하여 통신 시스템에서 널리 사용되고 있다. 그러나 페이딩의 영향으로 인하여 수신 데이터에 연속적인 오류가 발생하게 되면 오류 정정 부호를 사용하더라도 이와 같은 연집 오류(Burst Error)의 정정이 어렵게 된다. 이런 문제점을 해결하기 위하여 오류 정정 부호화된 데이터의 순서를 일정한 규칙으로 재배열하여 송신함으로써 연집 오류를 랜덤 오류로 바꾸어 오류 정정이 가능하게 해주는 역할을 하는 인터리버가 사용된다[1].

일반적인 협력 통신(Cooperative Communication) 환경에서는 송신기에서 사용된 인터리빙 파라미터를 수신기에서 알고 있기 때문에 이를 이용하여 디인터리빙이 가능하다. 그러나 수신기에서 송신기의 인터리빙 파라미터 정보를 전혀 알 수 없는 비협력 통신(Non-cooperative Communication) 환경에서는 수신된 데이터만을 이용하여 인터리빙 파라미터를 추정해야 하며, 이와 관련한 많은 연구들이 진행되어 왔다[2]-[10].

인터리빙 파라미터 추정을 위해 사용되는 기본 개념은 오류 정정 부호의 선형 특성을 이용하는 것이다. 예를 들어, 블록부호의 부호어는 메시지와 패리티로 구성되고 패리티 비트들은 메시지 비트들의 선형 연산에 의해 생성되기 때문에 선형 특성이 나타나게 된다. 선형 특성이 존재하는 경우 부호어 길이의 정수배 크기의 행과 열을 갖는 정방행렬을 만들어 차원(Rank)을 구하게 되면 오류가 없다고 가정했을 때 패리티 비트의 개수 만큼 차원이 줄어 들게 된다. 이것은 특정 열에 항상 패리비 비트들이 정렬하게 되어 가우스 소거를 하게 되면 해당 열의 값들이 0이 되기 때문이다. 만약 정방행렬을 구성하는 행의 크기가 부호어 길이의 정수배가 되지 않으면 패리티 비트들이 정렬되지 않아 랜덤 데이터로 구성한 정방행렬의 경우와 동일한 차원 분포를 갖게 된다.

본 논문에서는 수신데이터로 구성한 정방행렬의 차원 분포가 다항 분포로 나타나는 특징을 이용하여 인터리빙 파라미터를 추정하는 알고리즘 [10]에 대해 임계값 변화에 따른 검출 확률 및 오경보 확률(False Alarm Probability)을 구하여 임계값과 추정 성능의 관계를 알아보고, 다항 분포의 확률 질량 함수(Probability Mass Function)를 이용한 인터리빙 주기 추정 성능을 레일리 페이딩 채널에서 모의실험을 통하여 분석한다.

Ⅱ. 인터리빙 파라미터 추정 알고리즘

인터리빙 파라미터 추정 관련 연구는 Burel[6]이 오류가 없는 환경에서 수신된 데이터를 인터리빙 주기만큼 쪼개어 만든 정방행렬에서 차원 부족(Rank Deficiency)이 나타나는 점을 이용하는 추정 방법을 제안한 것이 근간이 된다. 이 방법은 이상적인 채널을 가정한 알고리즘으로서 오류가 발생하는 경우에 그대로 적용할 수 없다는 단점을 가지고 있다.

Sicot[7]은 인터리빙 주기와 일치하는 행과 열 크기를 갖는 정방행렬을 구성하더라도 채널에서 오류가 발생하는 경우에는 오류 정정 부호의 패리티 비트로 구성된 열이 모두 0이 되지 않아 선형성이 나타나지 않지만 ‘거의’ 선형성을 보이고 있다는 점을 이용하여 GJETP(Gauss-Jordan Elimination Through Pivoting) 수행 후 해밍(Hamming) 무게를 구하여 인터리빙 주기를 추정하는 알고리즘을 제안하였다. 그러나 이 알고리즘은 채널상의 오류발생이 증가하게 되면 오경보 확률이 함께 증가하는 문제가 발생한다.

Choi와 Yoon[8]은 오류가 덜한 수신 데이터를 선별하여 구성한 직각행렬의 차원 부족 발생 여부로 인터리빙 파라미터를 추정하는 SES(Sifting Errorless Symbol) 알고리즘을 제안하였다. 이 방법은 인터리빙 주기를 임의의 자연수 L이라 가정했을 때 수신된 데이터를 L비트씩 묶어 하나의 행을 구성하고 이것을 다시 L+K 개 씩 쌓아 (여기서 K > 0 인 자연수) 직각행렬을 만들고 가우스 소거를 이용하여 차원을 구한다. 만약 구해진 차원이 인터리빙 주기라고 생각한 L 보다 작아 차원 부족이 발생하면 L을 인터리빙 주기로 판정한다.

이후 랜덤 이진 데이터의 차원 분포와 쿨백 라이블러 발산(Kullback-Leibler Divergence: KLD)을 이용하는 인터리빙 추정 방법이 제안되었다[9]. 수신데이터를 L×L 정방행렬로 구성한 후 이 행렬의 차원 분포와 랜덤 정방행렬의 차원분포를 비교하기 위해 쿨백 라이블러 발산값을 구한다. 쿨백 라이블러 발산은 두 확률 분포의 유사 정도를 비교할 수 있는 기준으로 사용된다. 만약 수신데이터를 인터리빙 주기와 같은 크기의 행과 열을 갖는 정방행렬로 구성했다면 랜덤 이진 정방행렬의 차원과는 다른 분포를 갖게 되며, 그렇지 않은 경우에는 랜덤 이진 정방행렬의 차원 분포와 유사하게 나타날 것이다. 각각의 경우 쿨백 라이블러 발산 값이 달라지며 이러한 특징을 이용하여 인터리빙 주기가 추정 되었는지를 판단하는 알고리즘으로 GJETP와 SES 의 추정 성능보다 우수한 성능을 보인다.

Ⅲ. 다항분포의 확률 질량 함수를 이용한 인터리빙 주기 추정 알고리즘

3.1 시스템 구성

인터리빙 파라미터를 추정하기 위한 시스템 구성은 그림 1과 같다. 소스 부호화된 데이터는 채널 부호기에서 오류 정정 부호화된 후 인터리버로 보내진다. 인터리버에서는 입력된 데이터의 순서를 일정한 규칙으로 변경하여 변조기로 보낸다. 변조된 신호는 페이딩 채널을 거쳐 수신기로 보내진다.

Fig. 1.

System model

비협력 통신환경에서는 송신되는 신호를 중간에서 간접적으로 수집하게 되며, 이러한 수집 환경에서는 일반적으로 LOS(Line of Sight) 신호 성분을 얻기 어렵기 때문에, 레일리 페이딩을 겪는다고 가정할 수 있다. 수신기에서는 복조된 데이터가 인터리빙 파라미터 추정기로 보내지고, 추정 알고리즘을 이용한 인터리빙 파라미터 추정이 완료되면 디인터리빙, 채널 복호 및 소스 복호를 거쳐 신호가 복원된다.

3.2 랜덤 이진 정방행렬의 차원 분포

본 논문의 추정 알고리즘은 수신데이터로 구성한 정방행렬의 차원 분포가 다항 분포를 나타내는 특징을 이용하며, 확률 질량 함수를 구하여 임계값과 비교함으로써 인터리빙 주기를 추정한다.

다항 분포의 확률 질량 함수의 계산에 필요한 각 차원들의 발생 확률은 랜덤 이진 정방행렬의 차원 분포 확률을 사용한다. 이를 위해 우선 랜덤 이진 정방행렬이 가질 수 있는 차원 분포에 대해 살펴본다. 갈루아 필드 GF(2)에서 0과 1로 구성된 랜덤 데이터를 L개씩 묶어 하나의 행을 구성한 후, L개의 행을 쌓아 만든 L×L 정방행렬에 대하여 L→∞ 일 때 이 행렬의 차원이 최대차원(Full Rank)에서 ϵ만큼 적은 값인 L-ϵ이 될 확률 P_ϵ 은 식 (1)을 이용하여 구할 수 있다[11].

$\[ P_{ϵ}=2^{-{ϵ}^2}\left[\prod _{i=ϵ+1}^{\infty }\left(1-2^{-i}\right)\right]\left[{\prod _{i=1}^{ϵ}\left(1-2^{-i}\right)}^{-1}\right] \]$

(1)

또한 식 (1)에서 ϵ = 0 인 경우에는

$\[ P_{ϵ=0}=\prod _{i=1}^{\infty }\left(1-2^{-i}\right) \]$

(2)

이 된다.

식 (1)과 (2)를 이용하여 랜덤 이진 데이터로 만든 L×L 정방행렬이 가질 수 있는 차원 및 발생 확률을 구해 보면 표 1과 같이 나타난다. 즉, 최대 차원이 될 확률은 0.288788, 최대 차원에서 1 만큼 줄어들 확률은 0.577576, 2 만큼 줄어들 확률은 0.128350과 같게 된다. 표 1에서 만약 ϵ이 4보다 큰 경우에는 발생 확률이 상대적으로 매우 작아져 큰 영향이 없기 때문에 고려하지 않는다. 또한 표 1에서 L이 20인 경우 L이 무한대일 경우와 거의 같은 값을 갖게 되므로 L이 20보다 큰 경우에는 근사적으로 L이 무한대일 때 값을 이용한다.

Table 1.

Distribution of the ranks of the random square matrices over GF(2)

3.3 다항분포의 확률 질량 함수를 이용한 인터리빙 추정

다항 분포는 다수의 결과를 갖는 사건에 대하여 반복 시행을 했을 때 발생하는 확률 분포이다. 예를 들면, 총 N번 어떤 시행을 했을 때 발생할 수 있는 사건을 E₁, E₂, ... , E_k 라 한다면, 각 사건들에 대한 확률 변수를 X₁, X₂, ... , X_k, 각 사건들이 발생할 확률을 p₁, p₂, ... , p_k 라 할 때 N번의 시행에서 사건 E₁이 x₁번, 사건 E₂가 x₂번, 그리고 사건 E_k가 x_k번 발생할 확률은 식 (3)과 같은 다항 분포의 확률 질량 함수로 표현이 가능하다.

$\[ \begin{array}{c}f\left(x_1,x_2,\dots ,x_k;N;p_1,p_2,\dots ,p_k\right)\hfill \\ =\mathrm{Pr}\left(X_1=x_1,X_2=x_2,\dots ,X_k=x_k\right)\hfill \\ =\left\{\begin{array}{c}\begin{array}{cc}\frac{N!}{\prod _{i=1}^k{x}_i!}\prod _{i=1}^k{p}_i^{x_i}\hfill & , when \sum _{i=1}^k{x}_i=N\end{array}\hfill \\ \begin{array}{cc}0& , otherwize\end{array}\end{array}\right.\hfill \end{array} \]$

(3)

여기서 $$ \sum _{i=1}^k{p}_i=1$$ 이다.

수신데이터를 이용하여 L×L 정방행렬로 만들어 차원을 구하면 최대 차원을 비롯한 여러 개의 차원값이 독립적으로 나타나기 때문에 이 행렬의 차원분포는 확률적으로 다항분포를 갖는다고 볼 수 있다. 따라서 표 1의 각 차원 값의 발생 확률과 식 (3)의 확률 질량 함수를 이용하면 수신된 데이터로 구성한 정방행렬이 갖는 차원 값들이 나타날 확률을 구할 수 있다.

표 1의 값들은 랜덤 데이터로 구성한 정방행렬에서 각각의 차원이 발생할 확률을 구한 것이므로 만약 수신 데이터로 구성한 정방행렬의 행, 또는 열의 크기가 인터리빙의 주기와 같은 경우에는 표 1의 차원 값들의 확률 분포와는 다른 값들을 갖기 때문에 이때 확률 질량 함수를 계산하면 랜덤 정방행렬의 경우보다 매우 작은 값이 나타나게 된다.

예를 들어 수신데이터로 구성한 정방행렬 100개에 대하여 차원을 구했을 때, 최대 차원 15회, 최대차원에서 하나 적은 경우 30회, 두 개 적은 경우 50회 등 표 2와 같이 나타날 확률 P 를 확률 질량 함수를 이용하여 계산하면 식 (4)와 같이 구할 수 있다.

Table 2.

Example of rank distribution of square matrix

$\[ \begin{array}{c}\mathit{P}=\frac{100!}{15!30!50!4!1!}{\left(0.288788\right)}^{15}{\left(0.577576\right)}^{30}\hfill \\ \times {\left(0.128350\right)}^{50}{\left(0.005238\right)}^4{\left(0.000047\right)}^1\hfill \\ \approx 1.96\times {10}^{-26}\hfill \end{array} \]$

(4)

식 (4)는 랜덤데이터로 만든 정방행렬의 차원 분포가 표 2의 실험 결과와 같이 나타날 확률이 매우 낮다는 것을 보여준다. 따라서 수신데이터로 만든 정방행렬의 차원이 표 2의 차원 분포가 되었다면 랜덤 정방행렬과 다른 분포를 갖는 경우라 볼 수 있으며, 예를 들면 선형성으로 인한 차원 부족이 나타나는 경우에도 해당 된다고 볼 수 있다.

이러한 특성을 인터리빙 주기 추정에 적용하기 위하여 수신된 데이터를 인터리빙 주기로 추정되는 길이인 L개씩 쪼개어 이를 다시 L개 쌓아 생성한 정방행렬의 차원을 구한다. 수신된 데이터를 바꿔가면서 반복적으로 이 정방행렬의 차원을 구하면 그 분포를 구할 수 있다. 이때 L이 인터리빙 주기와 다른 값인 경우에는 패리티와 메시지가 정렬되지 않게 되므로 행렬의 차원 분포는 표 1의 랜덤 정방행렬의 차원분포와 매우 유사한 분포를 나타내며, 이때 확률 질량 함수는 식 (4)의 결과보다는 훨씬 큰 값이 된다.

그러나 추정한 인터리빙 주기 L이 실제 인터리빙 주기와 같은 경우에는 패리티 비트와 메시지 비트들 간의 선형성으로 인하여 행렬의 차원이 줄어 들게 되어 표 1의 분포를 따르지 않으며 확률 질량 함수는 매우 작은 값이 나타나게 된다. 따라서 수신 데이터로 구성한 정방행렬의 차원분포에 대한 확률 질량 함수 값을 구해 특정 임계값과 비교하여 작을 경우 인터리빙 주기가 맞았다고 판단 할 수 있게 된다.

임계값이 높게 설정된 경우에는 검출 성공 횟수가 늘어나지만, 한편으로는 오경보 확률도 증가하여 추정 성공에 대한 신뢰도가 낮아진다. 반면 임계값이 낮아질수록 검출 확률은 낮아지게 되지만 오경보 확률도 낮아지게 되므로 추정 성공에 대한 신뢰도가 커진다. 따라서 적용하는 시스템의 특성에 맞춰 임계값을 조정함으로써 검출 확률과 오경보 확률을 제어할 수 있게 된다.

Ⅳ. 모의 실험 및 성능 분석

본 논문의 알고리즘 성능을 그림 2의 추정 방법을 사용하여 기존 방법들인 GJETP, SES, 그리고 KLD 알고리즘과 모의실험을 통해 비교 분석한다. 오류 정정 부호는 (7,4) 해밍 부호와 (15,11) BCH 부호를 사용하였고, 페이딩 채널은 레일리 페이딩을 가정하여 모의 실험을 진행하였다. 모의실험에 사용된 주요 파라미터들은 표 3과 같다.

Fig. 2.

Estimating method for interleaving parameter using probability mass function of multinomial distribution

Table 3.

Simulation Parameters

인터리빙 주기 추정 성공 여부의 판단기준이 되는 다항분포의 확률 질량 함수의 임계값을 정하기 위하여 임계값을 변화시키면서 검출 확률과 오경보 확률을 구하면 각각 그림 3, 4와 같이 나타난다.

Fig. 3.

Detection probability of interleaving Period

Fig. 4.

False alarm probability of interleaving period

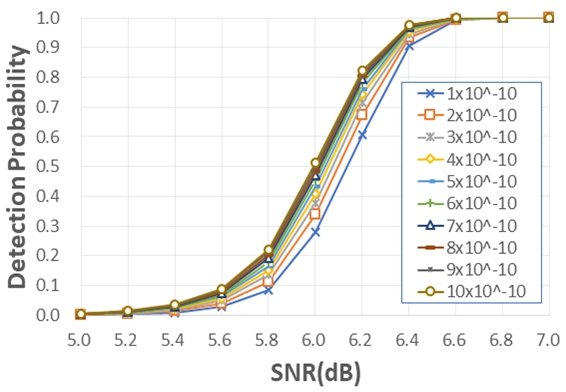
그림 3은 (7,4) Hamming 부호가 사용되고 인터리빙 주기가 35일 때, 임계값을 10^-10 부터 10^-9 까지 변화시키면서 신호 대 잡음비(Signal-to-Noise Ratio: SNR)별로 10,000회 실험을 반복하였을 때 주기 검출 확률과 오경보 확률을 구한 결과이다. SNR이 6dB인 경우, 임계값이 10^-10과 10^-9 일 때 검출 확률이 각각 0.28과 0.51로 검출 확률이 약 82% 증가하게 된다. SNR이 5.2dB보다 작을 경우에는 10^-10과 10^-9 일 때 모두 인터리빙 주기 검출에 실패하였고 6.6dB보다 큰 경우에는 10^-10과 10^-9 일 때 모두 주기가 100% 검출되어 이 SNR 구간에서는 임계값이 10^-10에서 10^-9로 변화하더라도 검출 성능에 큰 영향을 미치지 못하는 것을 알 수 있다.

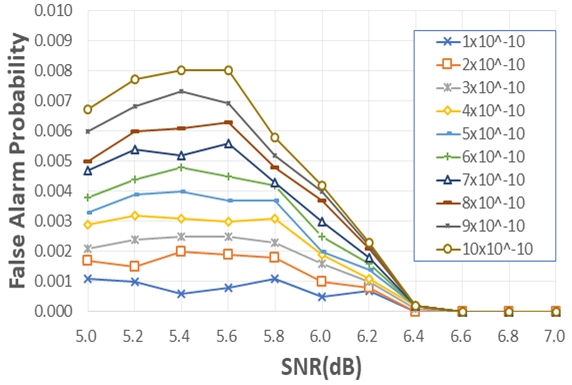
그림 4는 임계값에 따른 오경보 확률을 구하기 위하여 SNR을 변화 시키면서 10,000번의 반복 실험한 결과이다. 실험 결과 SNR 6dB에서, 임계값이 10^-10일 때 오경보가 7회 발생하였으나 임계값이 10^-9일 때는 42회 발생하여 약 6배 오경보 발생이 증가함을 알 수 있다. 따라서 임계값의 증가가 오경보 확률과 검출 확률을 모두 증가 시키므로 시스템에서 요구되는 추정 신뢰도를 고려하여 임계값을 결정하여야 한다. 본 논문에서는 오경보 확률을 최대한 억제하기 위하여 검출 확률이 낮아지더라도 임계값을 낮게 설정하여 모의실험을 진행하였다.

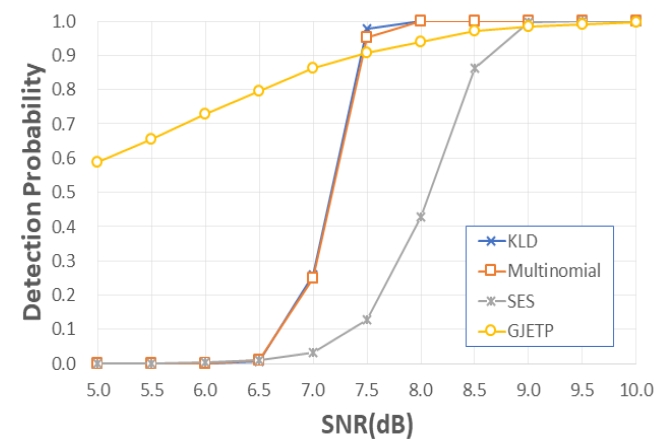
그림 5는 (7,4) 해밍 부호가 사용되고 인터리빙 주기가 35일 때 레일리 페이딩 채널에서 본 논문의 알고리즘과 기존 알고리즘들의 추정성능을 비교한 결과이다. 여기서 Multinomial은 본 논문의 알고리즘이며, GJETP, SES, KLD는 각각 [7], [8] 및 [9]의 성능을 나타낸다.

Fig. 5.

Detection probability with (7,4) Hamming code and interleaving period 35

본 논문의 알고리즘의 검출 성능과 KLD의 결과가 거의 동일하게 나타나 약 7.5dB 이상에서는 거의 100% 검출이 가능하였으며, SES 대비 검출확률 50%에서 약 1dB 정도 우수한 성능을 나타내었다. 본 논문의 알고리즘과 KLD 모두 행렬의 차원 분포를 비교하는 확률적 접근 방법으로서 다항분포의 확률 질량 함수와 쿨백 라이블러 발산 값을 각각 판단 기준으로 삼고, 오경보 확률을 최대한 억제하도록 임계값을 설정하여 검출 여부를 판단하기 때문에 두 알고리즘의 성능이 거의 같게 나오게 됨을 유추할 수 있다.

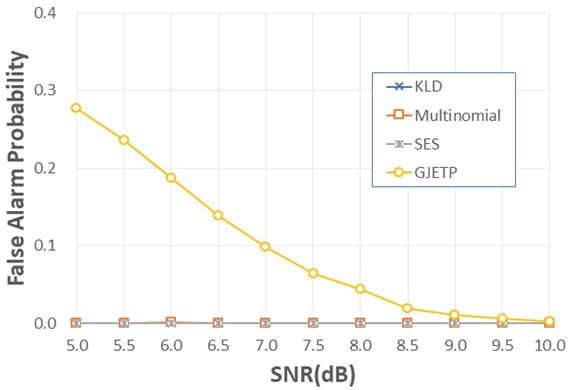
GJETP 알고리즘은 거의 100% 추정 확률에 도달하기 위해서는 9.5dB 이상의 높은 SNR이 필요함을 확인할 수 있다. 또한 낮은 SNR에서 검출확률이 다른 알고리즘들에 비하여 높게 나타나지만, 그림 6에서 볼 수 있듯이 다른 알고리즘의 오경보 확률이 거의 0인 반면에, GJETP 알고리즘은 8dB에서 0.29 정도의 확률로 다른 알고리즘 보다 상대적으로 높은 오경보 확률이 나타나는 것을 알 수 있다. 한편 KLD 에서는 로그 연산이 요구되고, 두 확률 값의 위치가 바뀌면 값이 달라지게 되어 거리 함수로 사용할 수 없으며, 다항분포 확률 질량 함수는 계산 복잡도가 증가하게 된다.

Fig. 6.

False alarm probability with (7,4) Hamming code and interleaving period 35

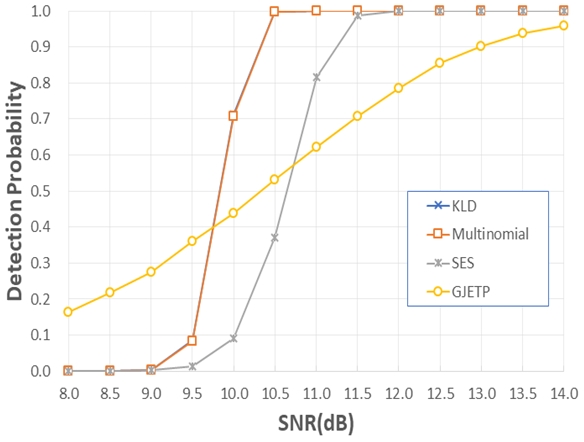
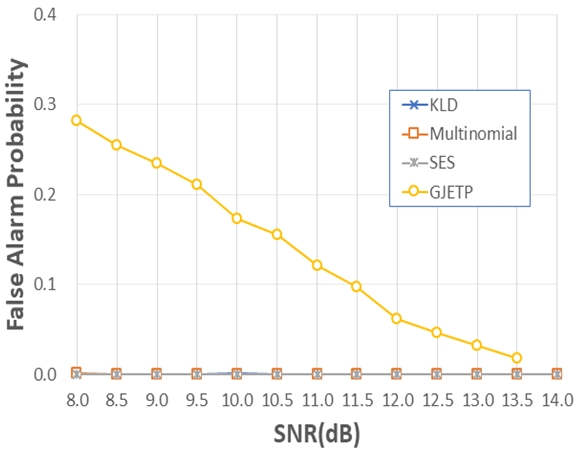
그림 7과 8은 (15, 11) BCH부호를 사용하고 인터리빙 주기가 30인 경우 검출 확률과 오경보 확률을 각각 모의실험을 통해 구한 것이다.

Fig. 7.

Detection probability with (15,11) BCH code and interleaving period 30

Fig. 8.

False alarm probability with (15,11) BCH code and interleaving period 30

그림 7에서도 본 논문의 알고리즘이 KLD와 성능이 거의 일치하여 겹쳐서 보이고, SES 알고리즘 보다 검출 확률 50%를 기준으로 약 0.9dB 우수한 성능을 보여주고 있다. 또한 SNR이 10.5dB 이상이면 주기 검출 확률이 거의 100%로 나타남을 알 수 있다. 반면, GJETP 알고리즘은 SNR이 14dB인 경우에도 100% 주기 검출이 되지 않으며, 그림 8에서와 같이 다른 알고리즘 대비 오경보 확률이 높게 나타남을 알 수 있다. 검출확률 90% 이상이 되기 위한 SNR과 해당 SNR 에서의 오경보 확률을 표 4에 나타내었다.

Table 4.

Summary of simulation results

Ⅴ. 결 론

본 논문에서는 레일리 페이딩 채널에서 다항분포의 확률 질량 함수를 이용한 인터리빙 주기 추정 알고리즘의 성능을 분석하였다. 본 논문의 추정 알고리즘 성능은 GJETP 와 SES 보다 우수하였고, 기존 알고리즘 가운데 가장 성능이 좋은 KLD 알고리즘의 성능과 거의 같게 나타났는데, 이것은 두 알고리즘이 정방행렬의 차원 분포를 확률적으로 비교하면서 오경보 확률이 최대한 낮게 나타나도록 임계값을 정하였기 때문이다.

또한 수신데이터로 구성한 정방행렬의 차원 값에 대한 확률 질량 함수값을 임계값과 비교하여 임계값보다 작은 경우 정방행렬의 행 또는 열의 크기를 인터리빙 주기로 판단하게 되므로 임계값을 높게 설정하면 검출 성능이 좋아지지만 오경보 확률도 함께 높아지게 된다. 따라서 시스템 설계 시 검출 성능에 대한 신뢰를 가질 수 있는 수준으로 임계값을 정해 오경보 확률을 제어 하여야 할 것이다.

향후에 본 논문의 알고리즘이 SNR이 낮을 경우에도 추정이 가능하도록 동적으로 임계값을 조절하거나 SNR이 낮은 구간과 높은 구간에서 각각 최적의 검출 알고리즘들을 복합적으로 사용하는 방법에 대한 연구가 진행되어야 할 것이다.

Acknowledgments

이 연구는 방위사업청 및 국방과학연구소의 재원에 의해 설립된 신호정보 특화연구센터 사업의 지원을 받아 수행되었음.

References

• S. B. Wicker, "Error control systems for digital communications and storage", Englewood Cliffs, NJ, USA, Prentice-Hall, p424-427, (1995).
• A. Valembois, "Detection and recognition of a binary linear code", Discrete Applied Mathematics, 111(1-2), p199-218, Jul.), (2001. [https://doi.org/10.1016/s0166-218x(00)00353-x]
• M. Cluzeau, "Block code reconstruction using iterative decoding techniques", In Proc. of ISIT06, Seattle, WA, USA, p2269-2273, Jul.), (2006. [https://doi.org/10.1109/isit.2006.261971]
• M. Marazin, R. Gautier, and G. Burel, "Some interesting dual-code properties of convolutional encoder for standards for self-recognition", IET Commun, 6(8), p931-935, May), (2012.
• Swaminathan, R, A.S. Madhukumar, N. W. Teck, and C. M. S. See, "Parameter estimation of convolutional and helical interleavers in a noisy environment", IEEE Access, 5, p6151-6167, May), (2017.
• G. Burel, and R. Gautier, "Blind estimation of encoder and interleaver characteristics in a non cooperative context", In Proc. of IASTED, Scottsdale, AZ, p275-280, Nov.), (2003.
• G. Sicot, S. Houcke, and J. Barbier, "Blind detection of interleaver parameters", Signal Processing, 89(4), p450-462, Apr.), (2009. [https://doi.org/10.1016/j.sigpro.2008.09.012]
• C. Choi, and D. Yoon, "Enhanced blind interleaver parameters estimation algorithms for noisy environment", IEEE Access, 6, p5910-5915, Mar.), (2018. [https://doi.org/10.1109/access.2017.2754638]
• C. Choi, and D. Yoon, "Blind interleaver parameters estimation using Kullback-Leibler divergence", Journal of KIIT, 15(12), p109-115, Dec.), (2017. [https://doi.org/10.14801/jkiit.2017.15.12.109]
• C. Choi, W. Jeong, S. Ahn, and D. Yoon, "Estimation of interleaver period using multinomial distribution", in Proc. of the KIDET 2017 Fall Conference, Seoul, Korea, p95-96, Oct.), (2017.
• E. M. Gabidulin, "Theory of codes with maximum rank distance", Problems of Information Transmission, 21(1), p1-12, Jan.), (1985.