콜센터 인입 콜량 예측을 위한 시계열 모델 비교 분석
초록
콜센터 운영자의 중요한 의사결정 작업은 비용을 최소화하면서 콜을 응대 할 수 있는 상담 인력의 적정 수준을 결정하는 것이다. 이를 위해서는 정확한 인입 콜량을 예측하는 것이 선행되어야 한다. 하지만, 국내외에 이에 대한 연구는 많지 않고 실제 콜센터에서는 담당자의 경험과 직관에 의지한 단순한 계산 방법이 여전히 주로 사용되고 있다. 이에 본 연구에서는 콜량을 예측하기 위한 다양한 기법과 사례들을 조사하고 최적화된 모델을 개발하고 검증한다. 요소분해 모형, 평활화 모형, ARIMA모형, 회귀분석 모형, 인공신경망 기반의 예측 모델을 만들고, 실제 콜 센터 데이터를 활용하여 최적화된 예측 모델을 개발하고 효용성을 검증한다.
Abstract
The critical decision-making task of the call center manager is to determine the appropriate number of agents who can respond to the call with minimal cost. To do this, it is necessary to predict the exact amount of incoming calls. However, there are not many studies on this at home and abroad. In actual call center, simple calculation method based on experience and intuition of the person in charge is still mainly used. In this study, we investigate various techniques and cases to predict call volume and develop and verify optimized models. We develop the call prediction model by using decomposition model, ARIMA model, regression model and artificial neural network based model, and fitting of optimized prediction model by using real call center data and verify its effectiveness.
Keywords:
call center, call arrival forecasting, wfm, ARIMA, ARIMAX, LSTM-RNN, regression, TBATS, STLⅠ. 서 론
콜센터는 최근 기업과 고객, 공공기관과 시민들 간의 핵심 커뮤니케이션 수단으로 자리매김하였다[1]. 정보안내, 고객 문의, 불만 접수/처리 활동을 비대면으로 수행할 수 있는 콜센터는 경영과 비즈니스 환경에서 중요성이 증가하고 있다[2].
비대면 채널은 최소한의 비용으로 고객 만족도를 높일 수 있는 가장 효율적인 수단이다[3]. 특히, 인터넷과 모바일 기술의 발달에 따라 전화 외에 이메일, 채팅, 인터넷 홈페이지 등 다양한 디지털 채널을 수용하여 컨택센터로 발전하고 있다[4]. 이런 측면에서 콜센터 운영은 기업 비즈니스에 큰 영향을 끼칠 수 있기 때문에 효과적인 운영이 중요시되고 있다.
고객과의 관계를 유지하고 기업을 대표해서 고객과 상대하는 책임을 지고 있는 콜센터는 최근 들어 수천 명 이상의 상담사를 가진 대규모 운영 조직으로 커져가고 있으며, 콜센터 산업은 노동 집약적이고 운영 예산의 60~80%가 인건비이다[2]. 고객의 전화를 응대하는 핵심 주체가 상담사이기 때문에 콜량과 처리 업무량에 맞춰 상담사의 인원이 결정된다. 콜센터에서 콜 응대는 실시간으로 이루어지기 때문에 전화를 응대할 충분한 상담사를 확보해야 한다[3]. 그렇지 않으면 고객 불만이 증가하고 영업기회를 잃어버리기 때문에 기업에 손실을 끼칠 수 있다[5]. 그래서 콜센터는 상담사 적정 인력 운영을 위한 계획을 수립하고 실행을 관리하기 위한 WFM (Workforce Management) 업무을 위한 전담 부서를 운영하며[3] 콜센터의 과거 콜 이력 데이터를 기반으로 콜 패턴을 분석하여 콜량을 예측하고, 시간대별 상담사의 필요 인원수를 예측하기 위 WFMS (Workforce Management System)의 활용도 늘어나고 있다.
하지만 한 상담사가 여러 개 유형의 업무 스킬을 동시에 보유하고 있어서 다수 유형의 전화 상담 업무를 응대하는 멀티 스킬을 적용하거나, 관리자의 경험에 기반한 이벤트 보정치의 설정에 주관적인 판단이 들어가기 때문에 WFM의 예측 결과는 신뢰하기 어려운 경우들이 자주 있다[3][6].
콜센터 운영자의 중요한 의사결정 작업은 비용을 최소화하면서 콜을 응대할 수 있는 상담 인력의 적정 수준을 결정하는 것이다. 이를 위해서는 정확한 인입 콜량을 예측하는 것이 선행 되어야 한다[7]. 하지만, 국내외에 이에 대한 연구는 많지 않고 실제 콜센터에서는 담당자의 경험과 직관에 의지한 단순한 계산 방법이 여전히 주로 사용되고 있다[3][8].
이에 본 연구에서는 콜량을 예측하기 위한 다양한 기법과 사례들을 조사하고 최적화된 모델을 개발하고 검증한다. 인입 콜에 영향을 줄 수 있는 인자들이 어느 정도 파악이 되거나 예측 가능한 변수가 있으면 인과 관계를 토대로 수리적 분석 모형을 만들어 분석하지만 인입 콜 예측의 경우 영향을 주는 인자를 찾기가 어렵고, 시간 변동적이고 확률적이며 기간 및 통화 유형에 따라 달라지고, 종종 외부 이벤트에 영향을 받기 때문에 불확실성이 높다[9]. 그래서 인과성과 무관하게 과거 데이터만으로 예측하는 시계열 분석을 많이 사용한다[10]. 최근에는 딥러닝을 활용한 시계열 연구도 활발하다[11].
예측(Forecasting)을 하기 위해서는 문제와 데이터 수집이 선행되어야 하며, 그 후 적당한 모델을 선택하고 예측하여야 한다[12]. 이에 본 연구에서는 실제 콜센터 데이터를 사용하여 통계 기반의 시계열 모델, 회귀분석 기반 예측 모델, 딥러닝 기반의 예측 모델들을 적용하여 최적 모델을 선택하는 과정을 제시하고, 적용 결과를 비교 평가한다.
Ⅱ. 관련 연구 및 배경 이론
2.1 콜량 예측 연구
J. W. Taylor는 2주 후의 콜량을 예측하기 위해 단변량 시계열 방법을 활용하였다[9]. Box-Jenkins 기법으로 보정한 ARIMA(Auto Regressive Integrated Moving Average)방법과 시계열을 분해하기 위한 홀트-윈터스의 확장을 통해 약 2~3일 전까지 예측할 수 있다는 것을 보여 주었다. 하지만, 다른 외적 요인이나 인자에 대한 분석이나 회귀 모델 등과의 비교는 없었다.
F. M. Bianchi 등은 모바일 기지국에 인입되는 호출 부하를 예측하기 위해 반향 상태 네트워크(Echo State Networks) 모델을 사용하였다[13]. 기존 접근법과 차이는 전화 인입량 외에 셀에 등록된 활동에 대한 추가 전화 기록을 외인 변수로 포함했고, 유전 알고리즘을 사용하여 파라미터를 최적화하였다. 하지만 이 연구는 콜량 예측이긴 하지만 모바일 기지국간의 콜 트래픽에 대한 데이터 예측으로 콜센터처럼 대기를 하는 시스템에서의 인입콜 예측은 아니라는 점에서 콜센터에 적용하기에는 한계가 있다.
R. Ibahim와 P. L'Ecuyer는 다양한 리드타임에 따른 콜량 예측 시도, 일간, 일자내의 상관관계에 따른 콜량 예측 모델을 개발하였다[10]. 다음날 예측보다 14일 이후 예측의 성능이 더 좋은 부분은 실무에 도움이 되는 의미 있는 연구였다. 하지만 1년간의 데이터만 수집, 년간 계절성에 대한 부분이나 추세에 대한 부분은 고려하지 못했다. 주로 하루나 주간 내에서 발생하는 변화가 다음 시간대에 영향을 줄 것이라는 부분에 대해서만 모델링 한 점은 장기적인 성장이나 추세가 있는 콜센터에는 적용이 어렵다는 한계가 있다.
Y. B. Kim 등은 시뮬레이션 도구인 ProModel을 통해 콜센터를 시뮬레이션하여 콜량을 예측하고 필요 인력을 산출하는 모델을 개발하였다[14]. 국내에서 시뮬레이션을 통해 콜량 예측 및 상담사 인력 스케쥴링에 대한 초기 연구로써 의미가 있으나, 시뮬레이션에 대한 구체적인 프로세스 정의가 없으며, 인입량이나 상담사 인력 예측의 정확도에 대한 검증이 전혀 없는 점은 아쉬운 부분이다.
W. Baek과 N. G. Kim은 데이터마이닝 기법인 의사결정트리를 이용하여 보험사의 콜량을 예측하였다[3]. 국내에서는 보기 드문 콜센터 콜량 예측 연구이며, 실제 콜센터의 데이터를 활용하고 기존에 콜세터에서 콜량 예측용으로 사용하던 WFM과의 비교를 통해 일부 업무에서 데이터마이닝 기법의 우수성을 입증한 부분에서 연구 의의가 있다. 하지만, 평가지표가 모호한 부분이 있으며, 자동차 보험사의 업무 특성을 기반으로 한 인자들을 의사결정트리 입력 요소로 사용하고 있어서 일반적인 콜센터에 적용하기는 어려운 한계가 있다.
S. Aldor-Noiman은 혼합된 포아송 프로세스 접근법을 통해 콜센터의 시스템 부하를 구하고, QED (Quality-Efficiency Driven) 체제에서 "Square Root Staffing" 규칙을 이용해 부하와 서비스 품질을 맞출 수 있는 모델을 제공한다[8]. 하지만 이 연구는 이스라엘의 텔레콤 회사의 특별한 요구사항에 최적화된 Mixed-Model이다. 6주간의 데이터만 학습하기 때문에 계절성이나 추세의 반영 부분은 반영하기 어려운 한계점이 있다.
콜인입은 일반적으로 Poisson 분포로 모델링 하는데 A. N. Avramidis 등은 이것에 대해서 실제 콜센터 환경에 맞게 다양한 예외상황에서도 동작할 수 있는 새로운 확률기반의 모델을 만들었다[15]. 하지만, 시뮬레이션을 통해 확률적 모델이 Robust한지에 대해서 관심을 가지는 연구이며, 대기 큐에서의 서비스 시간을 최소화하기 위한 연구로 콜량을 실제 예측하는 데 사용하기는 어려운 한계가 있다.
L. Brown 등은 일반적인 콜센터 대기모델인 M/M/N(Erlang-C) 모델에서 포기콜과 대기콜을 고려했을 경우 Erlang-A가 효과적인데 이를 실제 은행 콜 데이터를 통해 Erlang-A(M/M/N+M)로 모델링 하는 것이 가장 근접했음을 보여주었고 이를 콜센터 용량산정에 활용할 필요가 있음을 설명하였다[16]. 하지만, Erlang-A를 활용해 포기율, 대기시간의 성과 지표를 최적화하는 연구이기 때문에 콜량의 예측에 사용은 어렵다.
B. H. Andrews와 S. M. Cunningham는 아웃 도어 용품 및 의류 소매 콜센터의 전화 상담사를 위한 효율적인 인력 배치를 위해 콜량 예측 모델을 연구하였다[6]. ARIMA 전달 함수 방법론을 사용하여 계절적 패턴을 반영하고 휴일 및 광고 개입을 비롯한 독립 변수의 영향을 크게 받기 때문에 35개 이상의 외부 인자에 대한 시계열 데이터를 모델링했다. 모델의 향상된 정밀도는 향상된 스케줄링 효율성을 통해 매년 30만 달러를 절약 할 것으로 추산하였다. 콜량 예측을 통한 비즈니스 성과를 실증적으로 연구한 부분이 중요한 의미가 있다. 하지만 예측 모델 보다는 콜센터 콜 예측이 비즈니스 측면의 수익성에 대한 경제성 분석 중심이기 때문에 정확한 ARIMA 모델에 대한 설명이 없는 점이 아쉽다.
M. E. Jalal 등은 딥러닝 기법인 RNN(Recurrent Neural Network)를 사용하여 콜량을 예측하였다[5]. RNN을 사용하였을 때 실제 콜센터 데이터에서 콜량을 예측하는 것이 가능하다는 것을 보여주었다. 하지만, 기존의 다른 기법들과의 비교가 전혀 없다. 콜센터의 특성상 계절성이나 추세에 따라 시계열의 특성이 다른데 어떤 특성을 가진 콜센터인지 콜인입량에 대한 시계열적 분석이 없어서 일반화하기 어려운 한계가 있다.
2.2 분해(Decomposition) 모형
시계열 데이터는 추세, 계절성, 주기성 분해하여 패턴을 분석 할 수 있고, 이것을 통해 예측의 정확성을 높일 수 있다.
| (1) |
여기서 yt는 시계열 데이터, St는 계절성 요소, Tt는 추세-주기 요소, Rt는 잔차이다. 시계열을 분해하는 기법은 1920년대부터 많은 방법이 연구되었으며, 그 중 Celevland 등이 개발한 STL(Seasonal and Trend decomposition using Loess)이 매우 강력한 방법으로 알려져 있다[12][17]. STL은 월별, 분기별 뿐 아니라 모든 계절성을 다룰 수 있으며, 계절 요소가 시간에 따라 변동 되는 것을 허용하고, 특히, 특이값에 대한 영향도에 강건한 특성을 가지고 있다.
2.3 다중 계절성 지수 평활 모형
평활화(Smoothing)는 시계열 자료에 내포된 변동이나 불연속성을 약하게 하여 시계열 자료 내부의 추세 변동을 파악하여 예측하는 방법이다.
그중 지수 평활화 기법은 1950년대에 제안된 기법으로 이동평균 평활법에 시간에 대한 가중치를 부여한 것이다. 지수 평활법은 분석 대상 시계열 자로 N항에 대해서 가중치를 부여한 가중 평균을 산정하여 시계열 자료를 평활화하는 분석 방법이다[11]. 그 이후 시간에 따른 증가나 감소 추세를 고려한 지수평활 모형이 Holt에 의해 제시되었으며, Winters는 Holt 모형에 계절성을 고려한 모형을 추가하였다.
최근에는 De Livera 등이 개발한 다중 계절성 지수평활모형인 TBATS(Trigonometric, Box-Cox transform, ARMA errors, Trends, and Seasonal components)[18]이 기존 모형이 다루지 못했던 한계점들을 보완 하면서 전력 수요 예측 등에 사용되고 있다[19]. TBTAS는 기존 모델에서 지수평활모형으로 추세를 추정하고, 지수 평활모형의 오차항을 ARMA모델로 가정하고, Box-Cox 지수변환을 통해 종속변수의 비선형성을 개선하고, 다중 계절성을 위해 푸리에 변환을 통해 계산 속도를 향상 시켰다.
이로 인해 완전 자동화된 방식으로 푸리에 항, 지수 평활화 모델, Box-Cox 변환을 사용하여 다중 계절성이 있는 데이터에서도 계산시간이 우수하고 좋은 결과를 나타낸다[12][19].
2.4 ARIMA 모형
시계열 분석은 과거 시간에 관측된 데이터를 기반으로 미래에도 유사한 형태로 반복될 것으로 가정하고 과거 관측치의 상호 관계를 모형으로 구축하여 미래의 값을 예측하는 것이다[20]. 대표적인 시계열 방법으로 Box와 Jenkins가 시계열 오차항의 추정값이 편의되지 않는 모형으로 개발한 ARIMA 모형이 있다.
ARIMA는 자귀회귀 모형(AR)과 이동평균 모형(MA)으로 구성되며, 정상시계열을 만들기 위해 차분을 한다. 자귀회귀모형은 현재의 시계열이 과거 관측값으로 설명된다는 것이고, 현재의 오차항(White Noise)이 과거 오차항의 함수형태로 나타낼 수 있을 때 이를 이동평균모형으로 설명할 수 있다는 것을 의미하며 식 (2)로 표현된다.
| (2) |
여기서 yt는 t시점의 시계열 값이며, φ는 자귀회귀계수, θ는 이동평균계수, w는 오차항 또는 White Noise를 의미하며, p는 자기회귀부분의 차수, q는 이동평균부분의 차수이다.
ARMA모형은 시계열이 정상성(Stationary)을 가지고 있다고 가정한 상태에서 분석 가능한 모형이다. 하지만, 많은 시계열들이 정상성을 가지지 않는 경우가 많다[20]. 비정상 시계열의 정상화를 위해 차분이나 계절차분을 통해 회귀 추세나 계절적 변동을 제거해야 한다. 비정상 시계열을 ARMA모형으로 분석하기 위해서 정상 시계열로의 변환이 필요하다. 차분의 수행이 포함된 방식이 바로 ARIMA 모형이다. ARIMA의 I(Integration)는 차분을 의미한다[12]. 비정상 시계열에서 차분을 통해 계절 변동이나 추세요인을 제거하여 정상성을 가지는 시계열로 전환한다. 수식은 식 (3)과 같다. 여기서 y'은 차분된 시계열이며, 차분의 차수는 1 이상도 가능하다. 즉, 1회의 차분으로 여전히 비정상성을 가질 경우 한두 차례 정도 더 차분을 수행하면 정상성 시계열로 변환할 수 있다[20].
| (3) |
식 (3)을 Backshift 연산자를 사용해서 표현하면 아래식과 같다. Backshift 연산자 B는 시계열 데이터를 Lag에 대한 변수로 변환해주어 차분을 표현하는데 유용한 기법이다.
| (4) |
p : 자귀회귀 차수
d : 차분의 차수
q : 이동평균의 차수
B : Ba yt = yy-a, backshift operator
시계열 자료가 계절성을 가지는 경우에는 추세변동의 제거를 위해 계절 변동을 제거해야 한다. 동일한 주기, 요일 등의 관측값에 높은 상관관계를 갖는 주기성, 계절성(Seasonality)을 가지면 정상 시계열로 변환하기 위해 추세변동 제거에 필요한 차분 외에 계절성 제거를 위한 계절 차분이 필요하다. 이를 이용한 모형이 차수가 (p, d, q)(P, D, Q)s인 계절 ARIMA 모형이다. P는 계절 자귀회귀차수, D는 계절 차분 차수, Q는 계절 이동평균 차수, s는 계절 주기이다.
| (5) |
| (6) |
2.5 회귀분석 기반 시계열 예측
회귀모형은 데이터를 설명할 요인 값이 있을 경우 회귀식을 이용해 예측이 가능하지만, 그렇지 않은 시계열을 데이터에 대해서는 Time Lag을 이용해서 회귀식을 만들어 예측을 한다. 기본적인 개념은 yt값을 다른 시계열 값인 x와의 선형적인 관계를 유추하는 것이다[12][21].
| (7) |
여기서 β는 계수 값이고, ϵ은 잔차이다.
특히 회귀분석의 잔차가 자귀회귀성이 있을 경우 이를 다시 ARIMA모형을 통해서 분석할 수 있으며, ARIMA와 회귀분석을 두 가지 특성을 동시에 적용할 수 있는 모델이 ARIMAX이다[22]. 즉, 회귀분석의 잔차에 ARIMA를 적용하는 것이다.
| (8) |
식 (8)은 식 (7)에서 잔차를 ηt로 변경한 식이다. 예를 들어 ηt가 ARIMA(1,1,1)를 따른다면 아래와 같은 ARIMAX 모델을 만들 수 있다.
| (9) |
여기서 각 변수는 아래와 같다.
y't = yt - yt-1,
x't,t = xt,i - xt-1,
η't = ηt - ηt-1
2.6 인공신경망 기반 시계열 예측
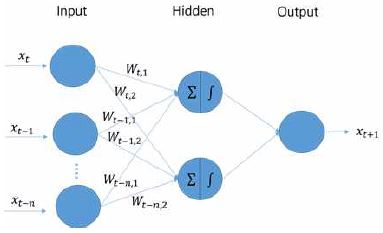
인공신경망기반의 시계열 예측은 TLFN(Time-Lagged Feed-forward Network)과 RNN 기반의 모델, 두 가지 방식으로 구현할 수 있다[23]. 전통적으로 시계열 예측을 신경망에서 구현할 때는 TLFN을 사용하였다[5].
TLFN은 n - k시점부터 n시점까지의 시계열 데이터를 입력 값으로 오류역전파 알고리즘을 사용하여 가중치를 학습하고, n+1시점의 시계열 데이터를 예측하는 기법이다.
| (10) |
식 (10)은 TLFN 모델을 설명한다. m은 은닉계층의 개수, n은 시점(Time Step), wj는 은닉계층과 출력계층을 연결하는 가중치 벡터, wji는 입력계층과 은닉계층을 연결하는 가중치 매트릭스, b0, b1은 바이어스이다. y(n)은 예측하고자 하는 시점에서의 시계열 값을 의미하며, x(n)은 n시점에서의 시계열 값이다.
최근에 딥러닝이 다양한 분야에서 좋은 결과를 나타내면서 딥러닝을 이용한 시계열 분석에 대한 연구가 증가하고 있다. 특히 음성인식, 번역과 같은 순서가 있는 데이터에 대한 분석에서 RNN이 좋은 성과를 내고 있다[24].
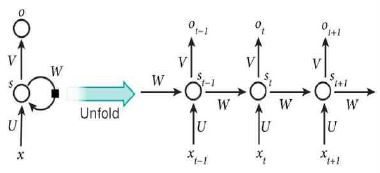
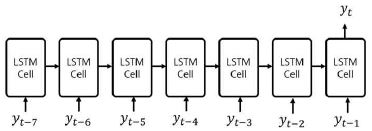
RNN은 순차적인 정보를 처리하는 데 적합하다. 아래 그림처럼 이전 노드의 출력값이 다시 입력계층으로 연결이 된다. 은닉계층은 "State Vector"를 통해 순차적인 데이터에서 과거의 정보를 유지한다. 이를 통해 과거의 정보가 현재에 영향을 미칠 수 있는 순차적 데이터의 처리에 용이하다[24]. 하지만, RNN의 내부 노드 수가 많아질 경우 기울기 소멸(Vanishing Gradient) 이나 기울기 폭발 (Exploding Gradient) 현상이 발생할 수 있다[25].
Diagram of TLFN
Diagram of RNN[24]
Diagram of LSTM cell[28]
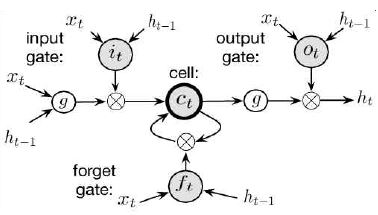
이를 근본적으로 극복하기 위해 나온 것이 바로 LSTM(Long Short-Term Memory)이다[26]. Standard LSTM은 순환 입력 값을 갖는 내부 메모리 노드와 입력 게이트, 출력 게이트로 구성 되어 있었다. 이를 통해 과거의 정보를 기억하고 활용하기에는 장점이 있지만 이로 인해 굳이 기억하지 않아도 될 과거의 정보가 영향을 미치는 문제가 발생한다. 이를 해결하기 위해 Forget Gate가 추가된 확장된 LSTM이 개발되었고[27] 현재 LSTM은 입력 게이트, 출력 게이트, 잊기 게이트로 구성이 되며, 순차데이터 예측에 상당한 강점을 보인다[25].
Ⅲ. 예측 모델 적용 및 평가
3.1 절차 및 문제 정의
콜센터의 인입 콜량을 예측(Forecasting)하는 기법은 사례에서와 같이 다양하다. 하지만 국내 콜센터 데이터를 통해 연구된 사례는 극히 드물다. 일반적으로 시계열 예측의 단계는 (1) 문제정의, (2) 정보수집, (3) 탐색분석, (4) 모델 선택 및 피팅, (5) 예측모델 적용 및 평가로 이루어진다[12].
예측하기 위해서는 먼저 예측하고자 하는 문제와 데이터 수집이 선행되어야 하며, 이에 맞는 모델을 선택하고 최적화해야 한다.
인입 콜량을 예측하기 위해서는 이에 맞는 데이터와 모델을 선정해야 한다. 본 연구는 예측을 위한 모델은 앞 장에서 설명한 회귀모델, Box-Jenkins의 ARIMA, 동적회귀모델, 인공신경망, 분해법 등 다양한 모델을 사용할 수가 있으며, 본 연구에서는 이들 기법을 사용하여 예측 모델을 만들어 결과를 비교하여 최적의 모델과 결과를 도출한다.
콜량 예측 모델의 결과 평가를 위한 지표는 다양한 방법이 존재하지만 본 연구에서는 직관적으로 예측결과를 인지 할 수 있는 MAPE(Mean Absolute Percentage Error; 식 (11))와 예측치의 오류 분포의 전체적인 부분을 잘 설명하는 RMSE(Root Mean Square Error; 식 (12))를 통해서 모델에 대한 평가를 할 것이다[29]. MAPE는 예측한 값과 실제 값의 차이의 절댓값에 대한 평균값으로 실제 값과 예측 오류사이의 비율을 제공함으로써 산업계에서 많이 사용되며, 전력량의 예측 등에서는 표준으로 자리 잡았다[30][31]. MAPE는 작은 값을 가질수록 예측 모형의 정확도가 높다고 평가할 수 있다[32]. RMSE는 MAPE가 가지는 선형적인 특성을 보완해주는 지표로 사용가능[31]하며 본 연구에서는 MAPE를 주 지표로 평가를 하고 오류 분포 파악을 위해 RMSE를 보조 지표로 사용하였다.
| (11) |
| (12) |
3.2 정보 수집 및 탐색 분석
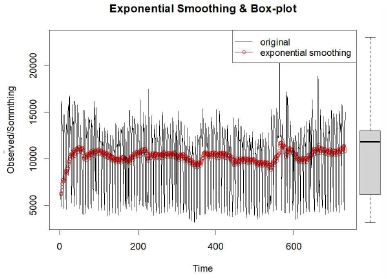
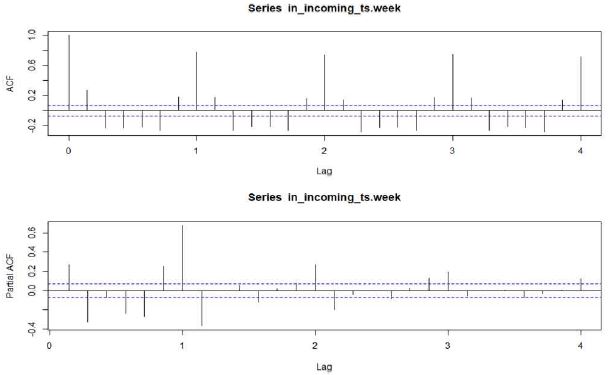
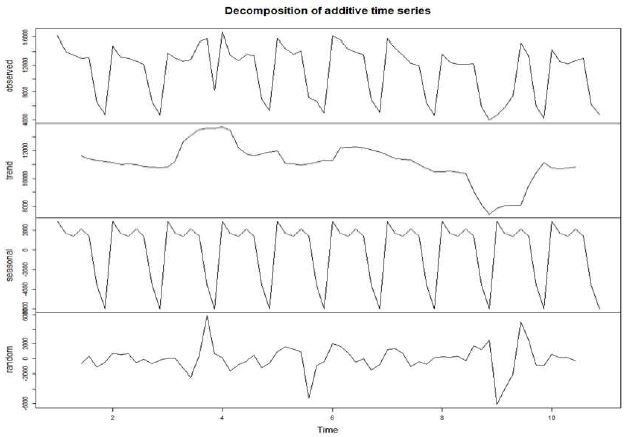
본 연구에서 사용할 콜 인입 데이터는 모 항공사 콜센터의 2년간 일일 콜 인입량을 사용하였다. 측정일수는 731일이다. 최소값은 3,196, 최대값은 23,050, 평균은 10,400이다. 콜에 대한 분해 결과는 그림 4에서 확인할 수 있다. 70일간의 샘플에 대한 분해결과를 보았을 때는 계절성이 있는 것은 시각적으로 충분히 확인 할 수 있다. ACF와 Partial ACF를 보면 Lag에 대한 의존 관계가 있음을 그림 5에서 도식적으로 확인 할 수 있다.
Call arrivals data and smoothing
ACF & partial ACF
3.3 모델 선택 및 피팅
본 연구는 선행연구의 다양한 모형들에 대해서 예측 성능을 최적화하기 위한 모형별 기법을 선택 하고 피팅 작업을 수행하였다.
Model-specific method and key fitting values
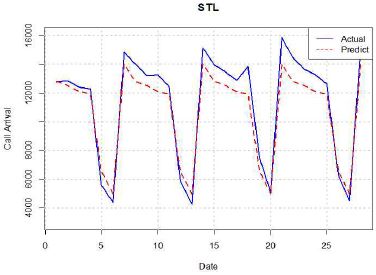
분해 모형을 수행하기 위해서 그중 가장 강력한 것으로 알려져 있는 STL기법을 사용하였다. STL은 추세와 주기성을 분해하여 분석하기 때문에 해당 시계열의 주기를 어떻게 설정하느냐가 중요한 요소이다. 그림 6을 보면 70일간의 계절성 그래프에서 10번의 반복적인 패턴을 보여주고 있어 7일 주기의 계절성이 있는 것을 시각적으로 확인 할 수 있다.
Decomposition of last 70 days sample
주기를 주간 단위인 7로 할 때와 월간 단위인 30.5로 할 때 성능은 7이 월등이 뛰어났다. R에서는 findfrequency()함수를 사용하여 시계열 데이터의 주기를 확인 할 수 있으며 동일하게 7로 확인되었다. 주기 7로 했을 경우 MAPE값이 8.01%로 상당히 좋은 값이 나오는 것을 알 수 있다.
STL forecasting
STL Result via frequency variation
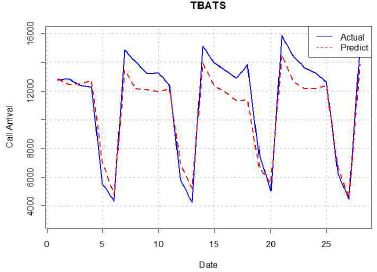
평활화 모형은 TBATS를 사용하여 모델링하였다. TBATS는 푸리에 급수(Fourier Series)를 이용하여 다중계절성을 고려한 모델을 만들기 때문에 주기를 여러 개 설정할 수 있다.
TBATS forecasting
TBATS result via multi-frequency
TBATS는 3중 주기성까지 설정을 할수 있으며, 2중 주기와 3중 주기에 대해서 실험해본 결과 2중 주기가 MAPE와 RMSE 지표에서 더 뛰어난 예측 성능을 나타내는 것을 확인 할 수 있다.
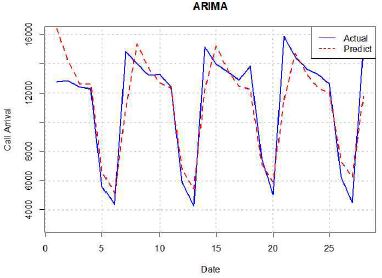
ARIMA의 경우 본 연구의 데이터가 주기성을 가지고 있기 때문에 추세분석과는 달리 이를 변화하지 않고 주기성을 고려하여 기존의 분석 모형을 적용하는 계절 ARIMA 모형을 적용하였다.
ARIMA는 R의 auto.arima 함수를 통해 최적값을 계산하였다. 최적 ARIMA(p, d, q)(P, D, Q)s 모델은 ARIMA(3, 0, 1)(2, 0, 0)[7]으로 계산 되었으며, AIC는 12665.29 AICc는 12665.5 BIC는 12701.73으로 측정 되었다.
ARIMA forecasting
회귀분석의 경우 주 단위 주기성의 데이터 반복특성을 분해를 통해 파악하였기 때문에 요일과 휴일 속성을 인자로 회귀분석을 수행하였다.
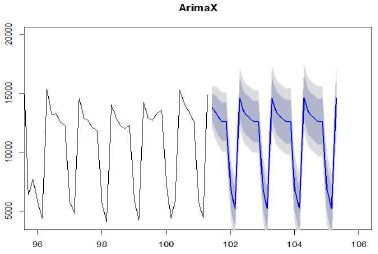
R2 값이 0.86으로 분석 변수에 대한 설명력이 높음을 알 수 있다. 하지만, 단순히 회귀분석으로 끝나지 않고 회귀식의 잔차에 해당 하는 부분에 대한 Durbin-Watson 테스트를 해본 결과 DW값이 0.585에 p-value가 0.001보다 적게 나와서 잔차가 자귀회귀성을 가지는 것으로 볼 수 있기 때문에 잔차에 대한 ARIMA분석이 가능함을 알 수 있다. 이에 ARIMAX로 추가적인 분석을 수행할 수 있었다.
Result of regression
ARIMAX forecasting
표 5의 결과를 보면 회귀분석과 회귀분석의 잔차에 대한 ARIMA분석을 추가로 수행한 ARIMAX 분석의 비교에서 MAPE는 유사한 수준이나 RMSE 측면에서 ARIMAX가 우수하다는 것을 확인 할 수 있다.
Regression forecasting
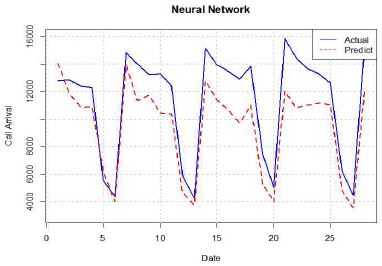
인공신경망 기반 시계열 예측을 위해 TFLN방식과 LSTM방식을 사용하여 실험을 하였다.
TFLN 방식의 경우 t시점을 예측하기 위해 t - p시점부터 t-1시점까지의 시계열 데이터를 입력 값으로 하기 때문에 적당한 p값을 구해야 한다. 하지만 계절성이 있을 경우 입력 값은 t - Ps가 된다. 그래서 p(Time lag), P(Seasonal Time lag), s(Seasonal 계수)를 구해야 한다. TFLN의 경우 Hyndman교수가 개발한 R의 nnetar함수를 사용하면 위 값들을 기본적으로 자동으로 계산을 해준다. 하지만 앞선 계절 ARIMA에서 도출한 p, P, s의 값과 개념이 동일하므로 auto.arima에 계산된 값과 nnetar에서 자동으로 계산된 값을 비교하여 좋은 RMSE와 MAPE를 얻은 모델에 사용하였다.
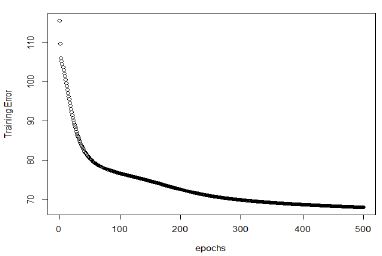
LSTM의 경우 wmtsa 패키지를 이용하여 학습하고 예측을 하였다. nnetar은 한 개의 은닉계층을 사용하고 노드의 개수와 Lag을 자동으로 최적화 해주기 때문에 별도의 하이퍼파라미터 설정이 필요 없다. 하지만 wmsta의 경우 자동으로 최적화 해주는 기능이 없기 때문에 입력 차원을 실험을 통해 최적 네트워크 모델을 찾아야 한다.
Compare model for TFLN
TFLN forecasting
본 실험에서는 그림 13과 같이 Time Lag을 7로 하여 입력 차원을 7로 학습하였을 때 가장 우수한 성능 값을 얻을 수 있었다.
LSTM learning curve
LSTM forecasting
LSTM application model
3.4 예측 모델 평가
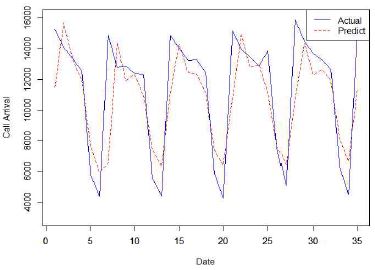
각 모델별로 701개를 학습세트로 하고 28일을 예측하여 그 결과를 분석하였다. 최종 모델별 적용 결과는 표 7과 같다.
Final result of forecasting
7가지 시계열 분석 기법 모델에 대한 적용 결과는 최종적으로 딥러닝 기반의 LSTM이 MAPE 값이 5.3%로 다른 모델에 비해서 상당히 우수한 성능을 나타내는 것을 확인 할 수 있다. RMSE의 값은 평균 오차에 대한 오도된 지표일 수 있기 때문에[29][33] 본 연구에서는 참고 지표로만 활용한다. (MAPE가 근접한 회귀모형과 ARIMAX의 비교에만 사용)
Ⅳ. 결론 및 향후 과제
본 연구는 콜센터 운영자의 중요한 의사결정 작업인 비용을 최소화 하면서 콜을 응대 할 수 있는 상담 인력의 적정 수준을 결정하기 위한 핵심 요소인 인입 콜량을 예측하기 위한 다양한 시계열 기법을 실제 콜센터 인입량 예측에 사용 가능하도록 모델링 하고 적합한 기법을 찾는 것이 목표였다. 특히 국내 콜센터에서 콜인입량에 대한 시계열 기반의 예측 연구는 거의 없었다.
본 연구는 현재 나와 있는 다양한 시계열 기법들을 실제 콜센터 데이터를 통해 검증하여 시계열 기법이 콜센터 콜량 예측에 사용 가능한지 비교 실험을 하였다.
MAPE측면에서는 LSTM이 우수한 결과를 도출하였다. 본 연구에 사용된 콜센터의 업무 특성상 요일에 대한 영향이 있기 때문에 Regression이나 ARIMAX가 다른 통계 기반 분석 보다는 성능이 좋게 나타나지만 딥러닝 방식의 LSTM이 MAPE측면에서 월등히 우수함을 알 수 있다.
시계열 예측은 모형에 데이터를 넣는 것으로 끝나는 것이 아니라 각 모형별로 최적 결과를 도출할 수 있도록 변수나 파라미터를 조절하는 것이 중요하다. 하지만, 기존의 연구에서 시계열 예측이 정말 중요한 콜센터 콜량에 대한 이런 연구가 없었기에 본 연구는 다양한 시계열 기법에 대해서 콜센터 데이터를 이용하여 피팅하고 결과를 비교하는 과정을 제시하여 유사한 문제를 해결하고자 하는 연구자들에게 도움이 될 것이라 생각한다.
콜센터처럼 콜량 예측이 중요한 곳에서 이런 시계열 연구는 매우 중요할 것으로 판단되며, 본 연구가 기폭제가 되어 더 많은 연구가 이루어지기를 기대한다.
본 연구에서는 일일 콜량을 예측 하였지만, 실제 콜센터에서는 시간단위나 30분 단위의 콜량 예측을 통해 더 정밀한 상담사 운영 관리를 하고 있다. 추후에는 이런 시간 단위의 콜량 예측 등을 통해 실무적으로 도움 될 수 있는 연구가 필요하다.
Acknowledgments
본 연구는 (주)이씨에스텔레콤의 지원으로 연구되었습니다.
References
- T. B. Nielsen, B. F. Nielsen, and V. B. Iversen, "Call Center Capacity Planning", Denmark, Technical University of Denmark (DTU), p14, Jan), (2010.
- Z. Askin, M. Armony, and V. Mehrotra, "The Modern Call Center: A Multi-Disciplinary Perspective on Operations Management Research", Production and Operations Management, 16(6), p665-688, Nov), (2007.
- W. Baek, and N. G. Kim, "A Case Study on Forecasting Inbound Calls of Motor Insurance Company Using Interactive Data Mining Technique", Journal of Intelligence and Information Systems, 16(3), p99-120, Sep), (2010.
- S. Sue, J. Fjermestad, and N. C. Romano Jr, "E-relationship marketing: changes in traditional marketing as an outcome of electronic customer relationship management", Journal of Enterprise Information Management, 17(6), p410-415, Dec), (2004.
-
B. H. Andrews, and S. M. Cunningham, "L. L. Bean Improves Call-Center Forecasting", Interfaces, 25(6), p1-13, Nov), (1995.
[https://doi.org/10.1287/inte.25.6.1]
- G. Koole, "Call Center Optimization", Lulu.com p1-3, Jan), (2013.
-
S. Aldor-Noiman, P. D. Feigin, and A. Mandelbaum, "Work load forecasting for a Call Center : Methodology and a case study", The Annals of Applied Statistics, 3(4), p1403-1447, Dec), (2009.
[https://doi.org/10.1214/09-aoas255]
- J. W. Tayler, "A Comparison of Univariate Time Series Methods for Forecsting Intraday Arrivals at a Call Center", Management Science, 54(2), p253-265, Feb), (2008.
- R. Ibahim, and P. L'Ecuyer, "Forecasting Call Center Arrivals: Fixed-Effects, Mixed-Effects, and Bivariate Models", Manufacturing & Service Operations Management, 15(1), p72-85, Sep), (2012.
- J. G. Lee, "R Program Recipes for Time Series Data Analysis", Bulls Book, p11-12, May), (2017.
- M. E. Jalal, M. Hosseini, and S. Karlsson, "Forecasting incoming call volumes in call centers with recurrent Neural Networks", Journal of Business Research, 69(11), p4811-4814, Mar), (2016.
- R. J. Hyndman, and G. Athanasopoulos, "Forecasting: principles and practice", OTexts, Oct), (2013.
-
F. M. Bianchi, S. Scardapane, A. Uncini, A. Rizzi, and A. Sadeghian, "Prediction of telephone calls load using Echo State Network with exogenous variables", Neural Networks, 71, p204-213, Sep), (2015.
[https://doi.org/10.1016/j.neunet.2015.08.010]
- Y. B. Kim, C. H. Lee, J. B. Kim, K. S. Lee, and B. C. Lee, "Enhancing the Performance of Call Center using Simulation", Journal of the Korea Society for Simulation, 12(14), p83-94, Dec), (2003.
-
A. N. Avramidis, A. Deslauriers, and P. L'Ecuyer, "Modeling Daily Arrivals to a Telephone Call Center", Management Science, 50(7), p193-222, Jul), (2004.
[https://doi.org/10.1287/mnsc.1040.0236]
- L. Brown, N. Gans, A. Mandelbaum, A. Sakov, H. Shen, S. Zeltyn, and L. Zhao, "Statistical Analysis of a Telephone Call Center : A Queueing-Science Perspective", Journal of the American Statistical Association, 100(469), p193-222, Mar), (2005.
- R. B. Cleveland, W. S. Cleveland, and I. Terpenning, "STL: A seasonal-trend decomposition procedure based on loess. Journal of Official Statistics", Journal of Official Statistics, 6(1), p3-73, Mar), (1990.
-
A. M. De Livera, R. J. Hyndman, and R. D. Snyder, "Forecasting Time Series With Complex Seasonal Patterns Using Exponential Smoothing", Journal of the American Statistical Association, 106(496), p1513-1527, Jan), (2012.
[https://doi.org/10.1198/jasa.2011.tm09771]
-
Y. I. Shin, and S. H. Yoon, "Electricity forecasting model using specific time zone", Journal of the Korean Data And Information Science Sociaty, 27(2), p275-284, Apr), (2016.
[https://doi.org/10.7465/jkdi.2016.27.2.275]
-
S. Y. Kim, H. Y. Jung, J. D. Park, S. M. Baek, W. S. Kim, K. H. Chon, and K. B. Song, "Weekly Maximum Electric Load Forecasting for 104 Weeks by Seasonal ARIMA Model", Journal of the Korean Institute of Illuminating and Electrical Installation Engineers, 28(1), p50-56, Jan), (2014.
[https://doi.org/10.5207/jieie.2014.28.1.050]
- K. W. Song, "ARIMA Time Series Analysis", GeumJeong(Busan), p25-26, Jul), (2005.
-
H. G. Sung, "Impacts of the Outbreak and Proliferation of the Middle East Respiratory Syndrome on Rail Transit Ridership in the Seoul Metropolitan City", Journal of Korea Planning Association, 51(3), p214-225, Jun), (2016.
[https://doi.org/10.17208/jkpa.2016.06.51.3.163]
-
Y. B. Dibike, and P. Coulibaly, "Temporal neural networks for downscaling climate variability and extremes", Neural Networks, 19(2), p135-144, Mar), (2006.
[https://doi.org/10.1016/j.neunet.2006.01.003]
- Y. LeCun, Y. Bengio, and G. Hinton, "Deep Learning", nature, 521(7553), p148-167, May), (2015.
-
S. M. Ahn, "Deep Learning Architectures and Applications", Journal of Intelligence and Information Systems, 22(2), p127-142, Jun), (2016.
[https://doi.org/10.13088/jiis.2016.22.2.127]
- S. Hochreiter, and J. Schmidhuber, "Long short-term memory", Neural Computation, 9(8), p1735-1780, Nov), (1997.
-
F. A. Gers, J. Schmidhuber, and F. Cummins, "Learning to forget: Continual prediction with LSTM", Neural Computation, 12(10), p2451-71, Oct), (2000.
[https://doi.org/10.1162/089976600300015015]
-
J. T. Chen, and D. L. Wang, "Long Short-Term Memory for Speaker Generalization in Supervised Speech Separation", Conference on Interspeech 2016, p3314-3318, Sep), (2016.
[https://doi.org/10.21437/interspeech.2016-551]
-
T. Chai, and R. R. Draxler, "Root mean square error (RMSE) or mean absolute error (MAE)? – Arguments against avoiding RMSE in the literature", Geosci. Model Dev, 7(3), p1247-1250, Jun), (2014.
[https://doi.org/10.5194/gmd-7-1247-2014]
-
W. G. Park, and S. Kim, "The Performance of Time Series Models to Forecast Short-Term Electricity Demand", Communications for Statistical Applications and Methods, 19(6), p869-876, Dec), (2012.
[https://doi.org/10.5351/ckss.2012.19.6.869]
-
H. S. Hippert, C. E. Pedreira, and R. C. Souza, "Neural Networks for Short-Term Load Forecasting: A Review and Evaluation", IEEE Transactions on Power Systems, 16(1), p44-55, Feb), (2001.
[https://doi.org/10.1109/59.910780]
- Y. S. Hwang, "A Hybrid Forecasting Framework based on Case-based Reasoning and Artificial Neural Network", Journal of Intelligence and Information Systems, 18(4), p43-57, Dec), (2012.
-
C. J. Willmott, and K. Matsuura, "Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance", Climate Resarch, 30(1), p79-82, Dec), (2005.
[https://doi.org/10.3354/cr030079]
1999년 2월 : 부산대학교 전기공학과(공학사)
2009년 11월 : 컴퓨터시스템응용 기술사
2013년 8월 : 서울과학기술대학교 IT정책전문대학원 산업정보시스템 전공 (공학석사)
2014년 3월 ~ 2016년 8월 : 서울과학기술 대학교 IT정책전문대학원 산업정보시스템전공 박사과정수료
2002년 8월 ~ 현재 : (주)이씨에스텔레콤 통신기술연구소
관심분야 : 컨택센터, 데이터마이닝, 최적화, 머신러닝, 시계열 예측
1986년 2월 : 서울대학교 산업공학과(공학사)
1988년 2월 : 서울대학교 산업공학과(공학석사)
1994년 2월 : 서울대학교 산업공학과(공학박사)
2003년 ~ 현재 : 서울과학기술 대학교 글로벌융합산업공학과 교수
1988년 4월 ~ 1991년 2월 : 동양 경제연구소 연구원
1999년 ~ 2001년 : University of Michigan Visting scholar
관심분야 : 최적화, IT서비스, 소프트웨어공학, 스마트그리드