최소 좁은 세상 셀룰러 유전알고리즘의 CUDA 병렬화

Ⅰ. 서 론

자연과 사회의 문제를 다루는 많은 모델이 병렬 처리가 가능하고, 인간의 뇌 역시 병렬처리 장치로 볼 수 있다. 2006년 NVIDIA의 CUDA(Compute Unified Device Architecture)가 발표되면서 병렬처리기술은 새로운 전환을 맞이하였다. CUDA는 고가의 슈퍼컴퓨터가 아니라 보통의 개인용 PC에서 병렬처리를 가능하게 한다. CUDA는 병렬처리를 위한 복잡한 하드웨어 및 프로그래밍 지식 없이 C 언어 등 고급 언어에 대한 지식만으로 쉽게 구현할 수 있다. 이러한 이유로 컴퓨터가 사용된 이후 오랫동안 여러 가지 환경에서 개발되어온 많은 문제들이 최근 수년 동안 CUDA를 사용하여 병렬화되고 있다.

복잡계 네트워크는 자연과 사회현상을 다루는 중요한 도구로 과학과 공학뿐 아니라 인문학과 사회과학의 분야에서 많은 연구가 진행되고 있다[1][2]. 복잡계 네트워크의 특성을 반영한 최소 좁은 세상 셀룰러유전알고리즘(SSWCGAs, Smallest-Small-World Cellular Genetic Algorithms)[3]은 대표적으로 병렬화가 가능한 알고리즘이다. 본 논문에서는 범용 GPU 플랫폼인 NVIDIA의 CUDA를 사용하여 SSWCGAs을 병렬화하였다. 2장에서는 SSWCGAs와 CUDA 병렬 프로그램의 구현을, 3장에서는 성능 분석을 하고 4장에서 결론으로 맺는다.

Ⅱ. CUDA 병렬 프로그램의 구현

이 장에서는 SSWCGAs의 CUDA 병렬 프로그램 구현에 대하여 설명한다.

2.1 최소 좁은 세상 셀룰러 유전알고리즘

좁은 세상 네트워크는 임의 네트워크의 일종이다[2]. 임의 네트워크는 두 노드 사이의 경로 길이가 짧고 클러스터링 계수 역시 매우 작다. 하지만 좁은 세상 네트워크는 대부분의 이웃 노드들이 서로 연결되어 있으며, 임의의 두 노드가 짧은 단계 만에 도달할 수 있는 경로를 갖는 네트워크이다. 즉, 클러스터링 계수는 크면서, 상대적으로 임의의 두 노드 사이의 평균 경로 길이가 매우 짧은 것이다[2][4][5]. 최소 좁은 세상 셀룰러 유전알고리즘[3][6]은 셀룰러 유전알고리즘[7]의 모집단을 좁은 세상 네트워크 형태로 구성하여 높은 클러스터링 계수를 유지하면서 짧은 평균 경로 길이를 갖는 위상을 갖도록 한 것이다. 이것은 격자형 네트워크에 최소의 링크를 추가하고도, 높은 클러스터링 계수를 갖도록 하여 세부탐색 능력은 보통의 셀룰러 유전 알고리즘과 같지만, 상대적으로 짧은 평균경로 길이를 가지므로 멀리 떨어진 개체들의 유전적 상호작용이 활발하여 빠르게 전역 탐색이 이루어진다.

그림 1은 SSWCGAs의 수행 절차를 나타낸다[3].

Fig. 1.

Algorithm of the SSWCGAs

2.2 CUDA 계산 환경 및 병렬 프로그램의 인덱스 전환

병렬 프로그램은 순차 프로그램에서 반복을 병렬로 처리하여 속도를 개선하는 것이 가장 기본이다. 따라서 반복문의 인덱스를 전환하는 것이 효율적인 병렬 프로그램의 구현에 있어서 중요한 역할을 한다. 여기서는 CUDA 프로그램에서의 인덱스 전환에 대하여 설명한다.

GPU는 배열 형태의 쓰레드로 구성이 되어 있는 쓰레드 블록 단위로 병렬 계산을 하며 CUDA 환경에서는 하나의 명령으로 쓰레드 블록을 제어하는 SIMT(Single Instruction Multiple Threads)을 사용한다[8]. 일반적으로 데이터 도메인은 쓰레드 블록의 크기보다 크기 때문에 도메인을 쓰레드 블록 크기만큼의 서브 도메인으로 나눈다. 그림 2는 하나의 도메인과 쓰레드 블록의 관계를 나타낸다. 그림에서는 12×12 크기의 도메인을 크기가 3×4인 12(4×3)개의 쓰레드 블록으로 나누었으며, 각 쓰레드 블록에 할당된 서브 도메인을 병렬로 계산하여 쓰레드 블록의 크기인 12배의 이론적인 성능 향상을 보일 수 있다.

Fig. 2.

Grid(domain) and thread blocks(sub-domain)

다음은 CUDA 병렬 프로그램의 인덱스 계산 방식을 이용한 병렬 프로그램의 구현에 대해 설명한다. 그림 2와 같은 크기의 도메인과 쓰레드 블록을 사용할 경우, 쓰레드 블록 변수 blockDim.x blockDim,y의 값은 각각 4와 3이고 blockIdx.x는 0, 1, 2이고 blockIdx.y 는 0, 1, 2, 3이다. 쓰레드 블록 내에서의 각 쓰레드의 인덱스 값 threadIdx,x는 0, 1, 2, 3이고 threadIdx,y는 0, 1, 2이다. 따라서 도메인의 모든 요소들이 인덱스 계산을 통하여 사용될 수 있다.

그림 3은 돌연변이 연산을 병렬화한 것을 나타낸다. blockIdx와 threadIdx의 값들은 동시에 제공되기 때문에 프로그램에는 반복문 대신 도메인의 경계값을 비교하는 비교문으로 대체된다. k 반복문은 하나의 후보해에 대해 유전자 단위로 돌연변이 여부를 판정하는 것으로 도메인과는 상관이 없기 때문에 계속 존재하게 된다.

Fig. 3.

Parallelizing the mutation operation

2.3 최대값 및 배열의 합 계산 - 리덕션

모집단 전체의 적합도 합이나 최적 개체를 찾기 위해서는 모집단 전체 즉 도메인 전체를 대상으로 처리가 이루어져야한다. 도메인의 모든 값들에서 최대값을 찾거나 합계를 구하는 경우에, 여러 쓰레드 블록에 값들이 분산되어 있기 때문에 다른 쓰레드에서 계산한 값을 처리해야 한다.

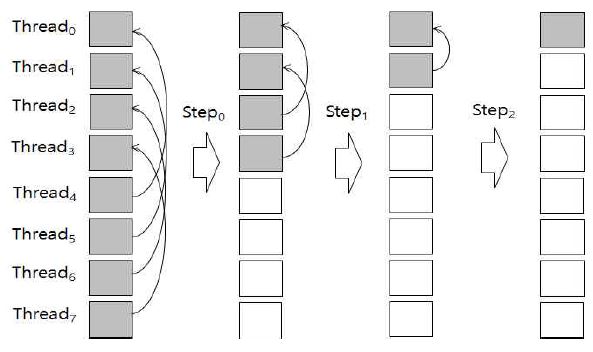
이를 위하여 본 논문에서는 리덕션 방식[8]을 적용하였다. NVIDIA GPU는 캐시메모리의 성능을 가진 쓰레드 블록 공유 메모리를 제공한다. 따라서 최적의 성능을 위하여 계산하고자 하는 도메인을 공유 메모리에 복사한 후 계산을 수행한다. 그림 4는 8개의 쓰레드를 가진 블록에서 처리한 값을 3단계 리덕션으로 처리하는 것을 나타낸다. 각 단계 별로(N/2#step-1)만큼 떨어진 쓰레드의 값을 사용하여 계산하고 log(N) 단계 이후에 최종적으로 Thread0에 원하는 결과를 저장한다. 각 쓰레드 블록의 계산 결과는 배열에 저장한 후에 CPU에서 최종적으로 계산한다.

Fig. 4.

Reduction method

그림 5는 리덕션 방식을 사용한 프로그램의 구현사례다. (a)는 적합도 합과 최적해를 구하는 순차 프로그램이고 (b)는 3단계 리덕션을 수행하는 CUDA 프로그램이다: (i) 먼저 계산의 대상을 공유 메모리에 복사한 후에 (ii) 리덕션 방식의 계산을 진행하고 (iii) CPU에서의 계산을 위하여 해당 값을 해당 배열에 복사한다.

Fig. 5.

Fitness sum and best sln. with reduction method

2.4 병렬 난수 프로그램

SSWCGAs은 난수를 주로 사용한다. 본 논문에서는 전체 도메인 단위로 임의의 수를 제공하는 난수 프로그램 방식[9]을 사용하였다. 이 병렬 난수 방식은 그림 6과 같이 최초의 도메인을 위한 난수는 순차적으로 계산하고 이후에는 도메인 단위로 난수를 병렬로 계산한다. 즉, 최초의 난수 도메인은 CPU 프로그램을 사용하여 순차적으로 계산하며 다음 도메인부터의 난수는 GPU에서 병렬로 계산하는 방식이다.

Fig. 6.

Calculation sequence of data domain for random #

그림 7은 난수를 계산하는 프로그램을 나타낸다. 순차 프로그램에서는 프로그램을 수행하면서 난수를 순차적으로 생성하지만 병렬 프로그램에서는 미리 쓰레드 블록 단위로 난수를 생성한 후, 병렬로 계산에 사용한다.

Fig. 7.

Fitness by reduction method

단순 유전 알고리즘을 병렬로 구현한 국내 외 사례는[10]-[13], 셀룰라 유전 알고리즘을 병렬로 구현한 사례는 [14]에 있다. 확률적 알고리즘을 병렬로 구현할 때는 난수를 어떻게 발생시키는지가 성능레 영향을 준다. 이 연구에서는 난수 발생의 효율을 높이기 위하여 난수 도메인을 그리드 상에서 병렬로 생성하여 도메인 계산을 병렬로 실행하도록 한 점에서 가존의 구현과 다르다. 또한 2.3절에 나타난 것과 같이 모집단을 분할하여 계산한 후, 개체의 전역 최대값을 계산하기 위하여 캐시메모리 역할을 하는 공유메모리를 사용하여 성능을 높였다.

Ⅲ. 성능 평가 및 분석

이 장에서는 본 연구에서 병렬로 구현한 최소 좁은 세상 셀룰러 유전알고리즘의 정확도와 수행시간을 평가한다.

평가를 위해 다중 6차 바이폴라 디셉티브 문제(MD)를 사용한다. 6비트가 모두 0이거나 1일 때 적합도 값 1을 갖는 6차 바이폴라 디셉티브 함수로 구성된 이 문제는 골드버그, 뎁 및 혼 등이 제안한 것으로 GA-hard 문제에 속한다[15]. 디셉티브 함수는 6비트로 표현된 개체에 대하여 스키마 경쟁에서 승자가 열성이 되도록 고안한 것이다. 문제에 포함된 디셉티브 함수의 개수가 n일 때 탐색공간의 크기는 2⁶ⁿ이고, $$ {\left(\left(\frac{6}{3}\right)+2\right)}^n$$개의 지역 최적해를 갖는다. 그 중에서 2ⁿ개만이 전역 최적해가 되므로 다루기가 매우 어려운 문제다. 예를 들어, 5개의 디셉티브 함수로 구성된 5중 6차 바이폴라 디셉티브 문제(MD5)는 개체의 크기가 30비트 스트링이며, 따라서 탐색공간의 크기는 2³⁰이고, 5,153,632개의 지역 최적해를 갖는다. 그 중에서 32개만이 전역 최적해이다. MD20은 20개의 디셉티브 함수를 부분 함수로 갖는 것으로 복잡도는 크게 증가한다.

3.1 최적해 성공률 평가 및 분석

본 논문은 SSWCGAs를 병렬로 구현하는 것이 주목적이므로 SSWCGAs 자체의 최적화 성능을 검증할 필요는 없다(SSWCGAs의 성능은 [3] 참조). 다만 병렬로 구현한 경우에도 최적해를 잘 찾는지를 확인할 필요가 있다. 여기서는 모집단의 크기를 달리해 가면서 100세대 내에 최적해에 도달하는 비율을 측정하여 병렬로 구현한 경우에도 최적해를 잘 찾는지를 평가한다. 이를 위해 MD20 문제에 대해 모집단의 크기를 달리해가면서 50회 실험하였으며, 교차율과 돌연변이율은 각각 0.85, 0.01로 하였다. 두 매개변수가 유전 알고리즘의 수행에 영향을 주지만 서로 다른 50개 모집단에 의한 평균 성능을 측정하므로 매개변수를 달리한 효과를 내포한다. SSWCGAs의 모집단은 논리적으로 격자형태이므로 모집단의 크기는 n × n으로 나타낸다. 표 1은 실험결과를 나타낸다. 실험에 사용된 GPU는 엔버디아텔사 C2075(코어당 1.15Hz, 448개의 코어로 구성)이다.

Table 1.

Success rate of parallel SSWCGAs

단일 프로세스에서 구현한 경우 모집단의 크기가 80x80을 넘으면 언제나 최적해에 도달하며 그때까지의 평균 세대수는 30.6~26.6임을 알 수 있다. 반면에 병렬로 구현한 경우 성공률은 다소 떨어지지만 모집단의 크기가 80x80을 넘으면서 96%이상의 비율로 최적해를 찾았고, 평균 세대수는 59.8~3.4임을 알 수 있다. 따라서 동일한 크기의 모집단에 대해 동일한 비율로 최적해를 찾을 수 있으므로 구현은 잘 되었다고 할 수 있다. 평균 세대수 편차에 대해서는 결론에서 다시 언급한다.

3.2 수행시간 분석

병렬로 구현한 SSWCGAs의 수행시간을 평가하기 위해 3.1과 같은 조건에서 모집단의 크기를 달리해가면서 100세대 수행시간의 50회 평균을 계산하였다. 실험 결과는 표 2와 같다. 실험에 사용된 쓰레드는 256(=16˟16)개로서 이는 리덕션 연산을 수행하기 위한 최대의 개수이다. 비교를 위하여 사용된 CPU는 인텔 i7-4770(3.4GHz)이다.

Table 2.

Average time for 100 generations(50 iterations, ms)

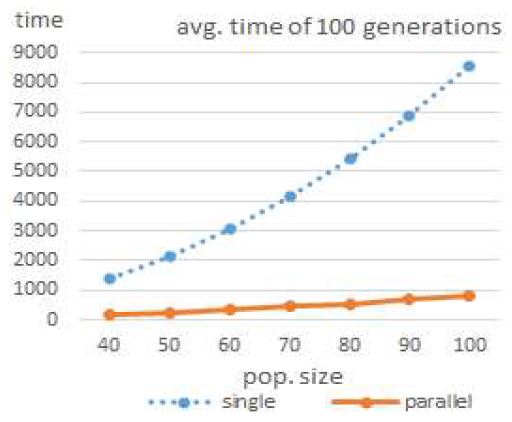
병렬로 구현하는 경우 100세대 수행시간 평균이 14%~9% 수준임을 알 수 있다. 그림 8은 수행시간 변화 추이를 나타낸다.

Fig. 8.

Average time for 100 generations

다음은 같은 조건에서 모집단의 크기를 달리해가면서 최적해에 도달하는 평균 수행시간을 계산하였다. 실험 결과는 표 3과 같다.

Table 3.

Average time to optimum(50 iterations, ms)

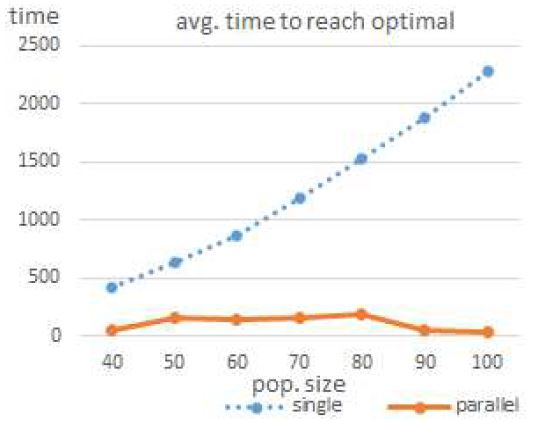
그림 9는 최적해에 도달하는 수행시간 변화 추이를 나타낸다. 모집단의 크기가 50x50인 경우를 제외하면 대략 10% 수준임을 알 수 있다. 이 경우 수행시간 비율의 편차가 큰 것은 앞과는 다르게 100세대 전에 최적해를 찾는 세대수에 편차가 크기 때문이다. 따라서 병렬로 구현하는 경우가 단일 프로세서로 구현하는 것보다 상대적으로 불안정하다고 할 수 있다.

Fig. 9.

Average run time for the best solution)

Ⅳ. 결 론

최소 좁은 세상 셀룰러 유전알고리즘은 격자 즉 그래프 형태의 모집단을 좁은 세상 네트워크로 구성하여 높은 클러스터링 계수를 유지하면서 짧은 평균 경로 길이를 갖는 위상을 갖도록 한 것이다[16]. 이렇게 하면 세부탐색 능력은 보통의 셀룰러 유전 알고리즘과 같으면서 상대적으로 짧은 평균경로 길이 때문에 빠르게 전역 탐색이 이루어진다. 이 연구에서는 이를 CUDA를 사용하여 병렬화 하였다.

성능을 평가하기 위해 20중 6차 바이폴라 디셉티브 문제 MD20을 사용하였다. 이 문제의 탐색공간 크기는 2^20×6으로 지역 최적해가 많은 매우 어려운 문제다.

평가 결과 동일한 크기의 모집단에 대해 동일한 비율로 최적해를 찾는 것을 확인 할 수 있었다. 또한 수행시간 측면에서도 대략 10% 내외의 시간에 최적해를 찾을 수 있음을 확인하였다.

모집단이 충분히 큰 90x90 이상의 경우 매우 빠르게(적은 세대수 만에) 최적해를 찾는데, 이는 지역 최적해가 지름길을 통해 중앙으로 이동하여 지역적으로 경쟁하는데 영향을 주기 때문으로 판단된다. 단일 프로세서에서 구현하는 경우 먼저 모든 후보해들이 지역적으로 경쟁한 후에 지름길을 통한 유전자 교환이 일어나는 반면, 병렬로 구현하는 경우 쓰레드 블록이 완료되는 시점에 유전자 교환이 일어나고 이것이 다른 블록 처리시 교환된다. 따라서 더 빠르게 좋은 후보해가 모집단에 퍼지게 된다. 이것은 병렬로 구현하는 경우 조기 수렴이라는 부작용이 발생할 수 있음을 의미한다. 실제로 병렬 SSWCGAs가 최적해를 찾는 비율이 2~4% 정도 낮은 것, 최적해에 도달하는 평균 수행시간의 편차가 큰 것과 관계될 것으로 판단되며, 추후 이에 대한 분석과 대응 방안에 대한 연구가 따라야 할 것이다.

References

• Reka Albert, and Albert-Laszlo Barabasi, "Statistical mechanics of complex networks", Rev. Mod. Phys., 74(1), p47-97, Jan), (2002.
• Ted G. Lewis, "Network Science Theory and Practice", Wiley, Apr), (2009.
• Taewon Kang, "Smallest-Small-World Cellular Genetic Algorithms", Journal of KIISE B:, 34(11), p971-983, Nov), (2007.
• D. Watts, and S. H. Strogatz, "Collective dynamics of small world networks", Nature(London), 393(6684), p440-442, Jun), (1998. [https://doi.org/10.1038/30918]
• D. Watts, "Small world: the dynamics of networks between order and randomness", Princeton, (1999).
• T. Nishikawa, A. E. Motter, Y. C. Lai, and F. C. Hoppensteadt, "Smallest small-world networks", Physical Review E, 66(4), p046139, Oct), (2002. [https://doi.org/10.1103/physreve.66.046139]
• D. Whitley, "Cellular Genetic Algorithms", Proc. 5th International Conference on Genetic Algorithms, p658, (1993).
• NVIDIA, CUDA, Compute Unified Device Architecture Reference Manual Version 5.0, NVIDIA Corporation, (2012).
• Youngtae Kim, and Gyuhyun Hwang, "Efficient Parallel CUDA Random Number Generator on NVIDIA GPUs", Journal of KIISE, 42(12), p1467-1473, Dec), (2015. [https://doi.org/10.5626/jok.2015.42.12.1467]
• Stefano Debattisti, Nicola Marlat, Luca Mussi, Stefano Cagnoni, Implementation of a Simple Genetic Algorithm within the CUDA Architecture, http://www.gpgpgpu.com/gecco2009/3.pdf.
• Il Jun Ahn, and In Kyu Park, "Design of Omok AI using Genetic Algorithm and Game Trees and Their Parallel Processing on the GPU", Journal of KIISE, 37(2), p66-75, Apr), (2010.
• Hyunsoo Park, and Kyungjoong Kim, "Systematic Evaluation of Island based Real-Valued Genetic Algorithm with Graphics Processing Unit", Proc. of Korea Computer Congress, 37(1(C)), p328-333, Jul), (2010.
• Byeongyong Hyeon, Ohsung Gwon, Soohwan Hyun, and Kisung Seo, "GPU Implementation of Genetic Algorithm", Proc. of Korean Institute of Intelligent Systems, 20(1), p3-6, Apr), (2010.
• Pablo Vidal, and Enrique Alba, "A Multi-GPU Implementation of a Cellular Genetic Algorithm, Evolutionary Computation (CEC)", 2010 IEEE Congress on Date of Conference, p1-7, Jul), (2010.
• D. E. Goldberg, K. Deb, J. Horn, Massive Multimodality, Deception, and Genetic Algorithms, IlliGAL Report No. 92005, Apr), (1992.
• TaeWon Kang, "Fault Tolerance Analysis of the Neural Networks of Scale-Free Network Architecture", Journal of KIIT, 11(7), Jul, 31), (2013. [https://doi.org/10.14801/kiitr.2013.11.7.151]